A wooden model of “Chess on the Dot”, designed and crafted by Joshua Chao.

This is an essay to detailedly elaborate the whole idea of “Chess on the Dot”, which is a chess variant with traditional chess rules but on the spherical chessboard. My other works “Globe Chess” and “Dot” are also related to this article.

How is it possible to play chess on a spherical chessboard with the traditional rules? Surprisingly, I found it’s not only possible but perfectly suitable.

Before I start to explain how, first I want to explain why I made this chess variant.

As you can see in Wikipedia “Chess variant” entry, there are many chess variants all over the world. People use different boards, pieces, rules or different number of players to create lots of funny new games.

When I saw these chess variants, I asked myself: If I’m going to create my own chess

variant, why do I do that after all? Is there any good reason to change such a perfect, classic board game?”

After research, I found that when Hindus created “Chaturanga”—the ancestor of chess-like board games—in the sixth century, perhaps their intention was to reconstruct an epic battle of armies (the word “Chaturanga” means“army” in ancient Hindu epic poetry) by a game on a flat board. At that time, Hindus believed that the world is a flat disc (see here), and it was a sure thing for them to use a flat board in the game.

Here I found a pretty good reason to create my own chess variant: Now we know that the world is in fact an orb, not flat anymore, so how about play chess on a real globe?

When I say “globe”, I mean an absolutely spherical form, like a ping pong ball. And then I made this wooden model:

A perfectly spherical chessboard, which can roll like a ball.

It’s not a cylinder or something similar to a ball. It’s a perfect sphere with no borders on it, just like our planet Earth.

That’s a good reason for me to make a chess variant now.

In order to call it briefly, I gave this spherical chessboard a short name, “Dot”.

It takes three steps to transmogrify a traditional, flat chessboard to a Dot:

1) Connect east and west borders, to create a tube.

2) Cover north and south ends, to create a cylinder.

3) Squeeze and bulk it up to a sphere.

This process is similar to transform a Mercator-projection world map into a terrestrial globe, just like the animation below:

The chessboard-Dot transmogrification

So, there are still 64 squares, with two extra “ends” on the surface of Dot.

The two ends are labeled “N” and “S”, they are two poles on the Dot. They are not squares, neither are they white nor black (so I use middle gray to color them). They exist to intact the surface of Dot, and keep all squares four-sided.

Since the two poles are not squares, an important principle rises: Pieces must not stay on the poles.

And as long as the poles are meant to intact the surface of Dot, another important principle rises: Pieces may pass the poles when they move.

By the way, the origin of the name “Dot” is from a photograph of planet Earth taken in 1990 by the Voyager 1 space-probe from a record distance of about 3.7 billion miles away from Earth, which is called “Pale Blue Dot”.

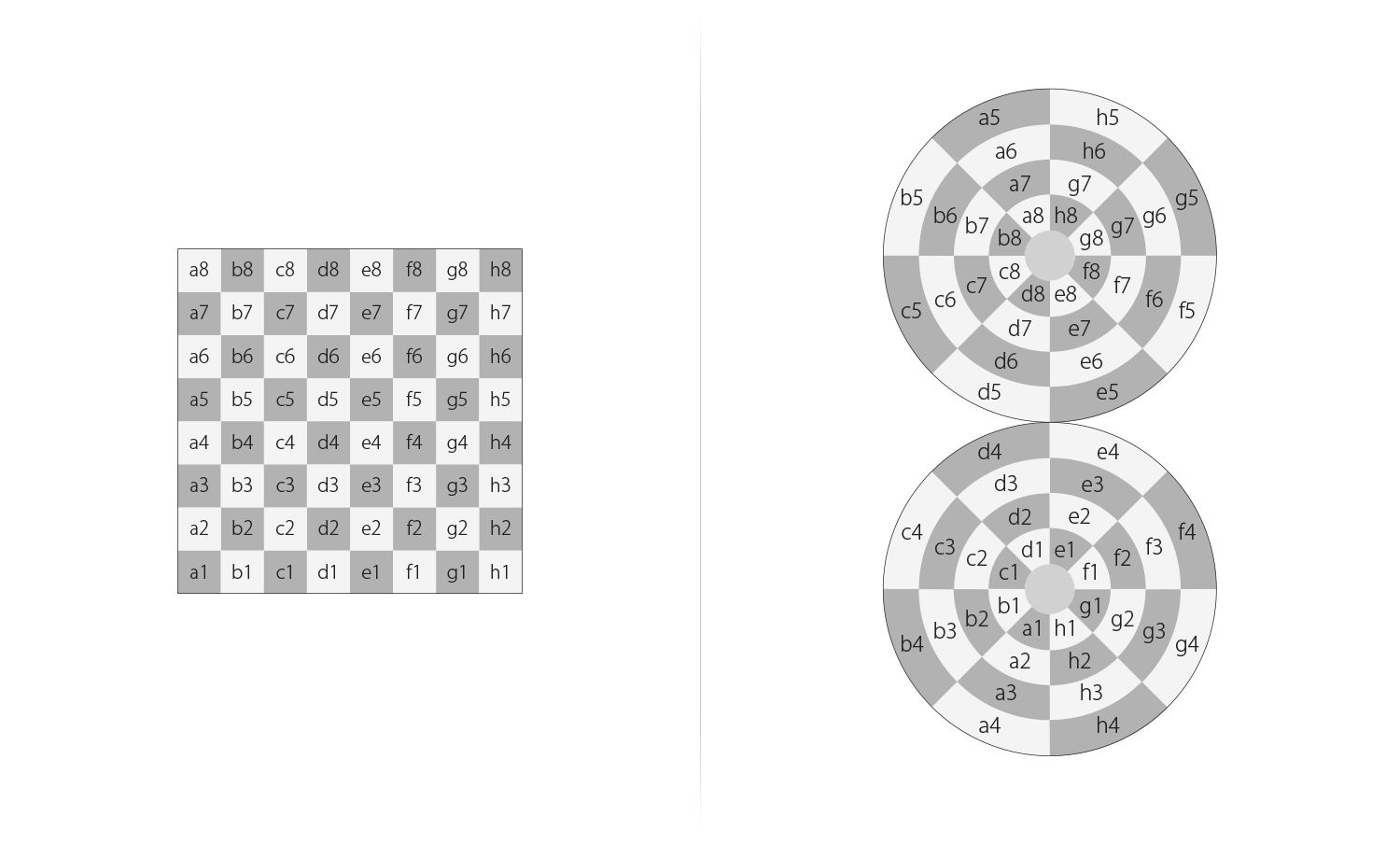
Back to the previously mentioned question: “How is it possible to play chess on a spherical chessboard with the traditional rules?” To answer that, first I need to exhaustively display all 64 squares on the surface of Dot in a 2-dimensional diagram, so I can draw pictures to explain it well.

It takes two steps to make a diagram of Dot:

1) Divide the Dot into two hemispheres by splitting it from the equator.

2) Use “Azimuthal equidistant projection” to project them as two circles.

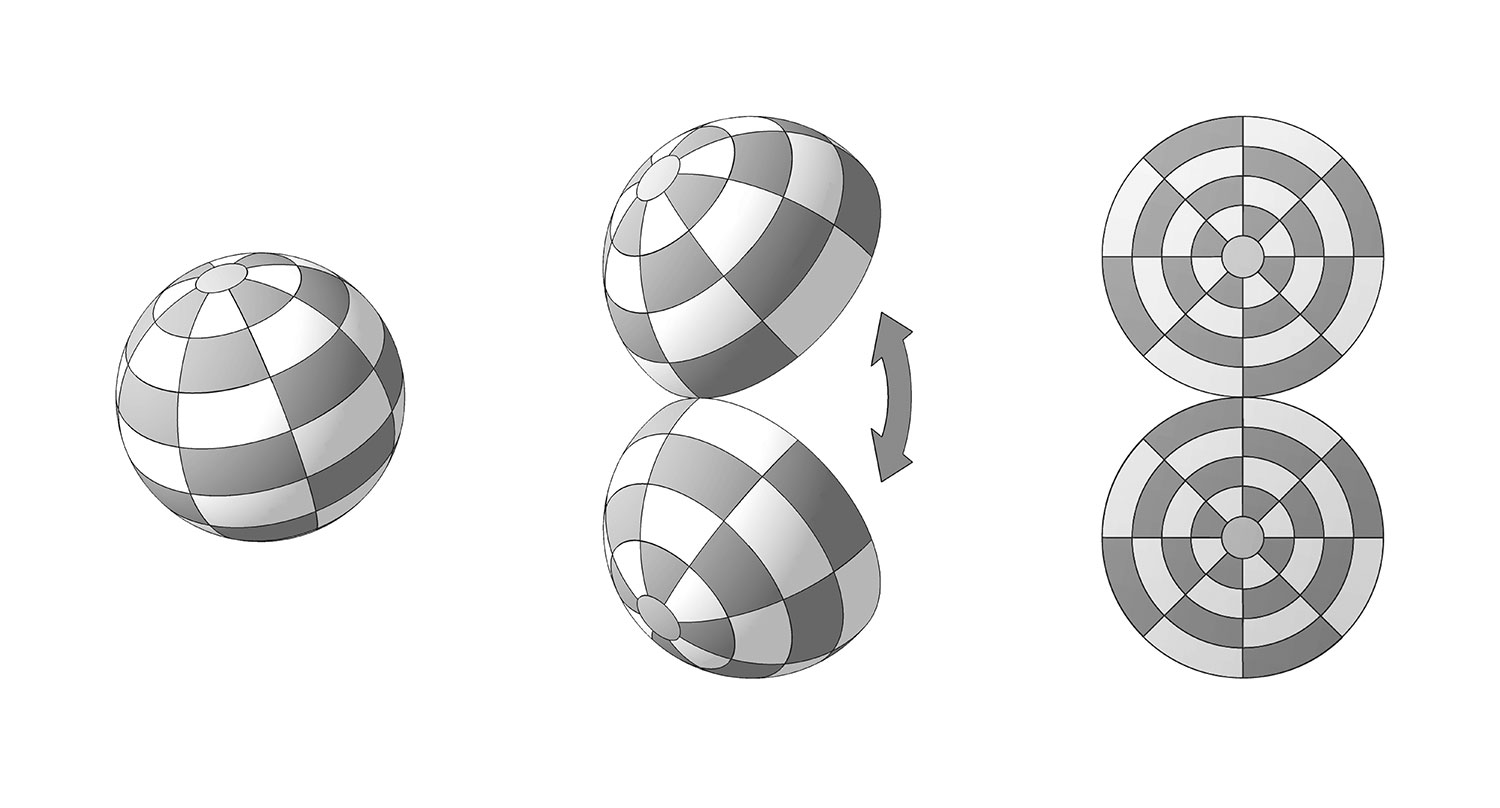
Make a diagram of Dot

In the diagram, the upper circle is the northern hemisphere and the lower circle is the southern hemisphere.

The circumferences of two circles are connected with a single point on the diagram, but they are actually full-connected as a single looped line (the equator) on the Dot. The animation below shows the relation of squares on two hemispheres more accurately.

The relation of squares on two hemispheres

In the future, imagine that the two circles of all diagrams are rotatable, just like the gear-wheel animation above.

Remember how the Dot is transmogrified from the flat chessboard? If the notation of every single square remains during transmogrification, the diagram with notation will look like this:

Notation of squares on the chessboard and the Dot

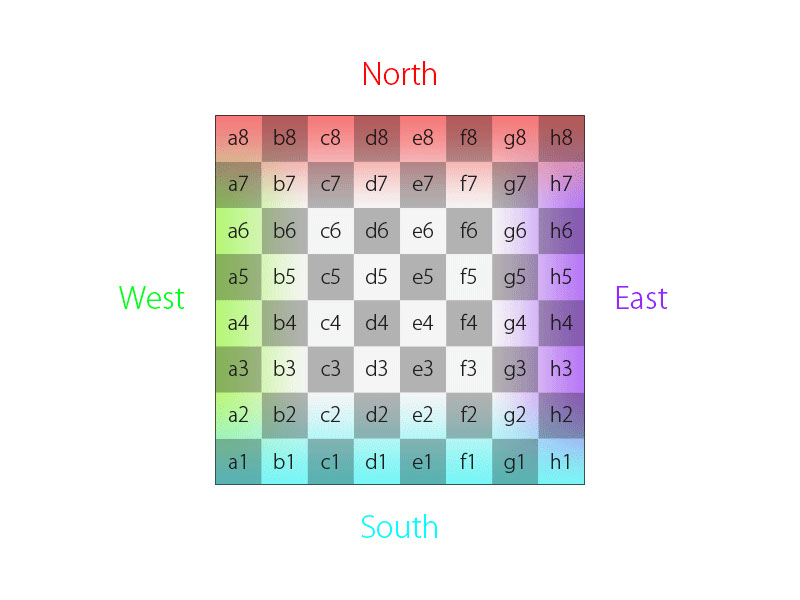
The principles of notation on the chessboard is: The horizontal “ranks” are noted with numbers 1 to 8. The vertical “files” are noted with letters a to h.

Likewise, the principles of notation on the Dot is: The “latitudes” are noted with numbers 1 to 8. The “longitudes” are noted with letters a to h.

The animation below shows the relation of noted squares on two hemispheres more accurately.

The relation of noted squares on two hemispheres

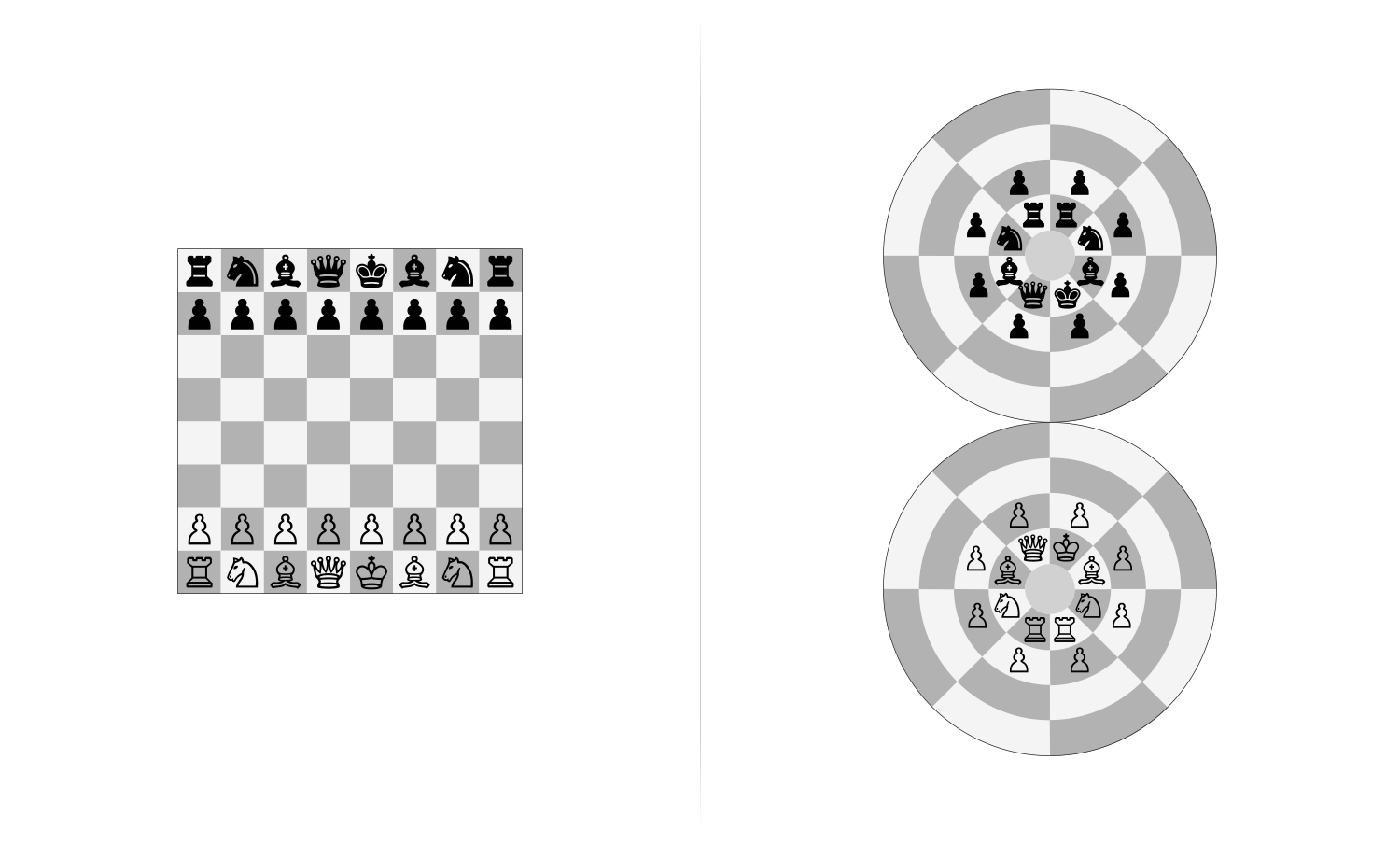
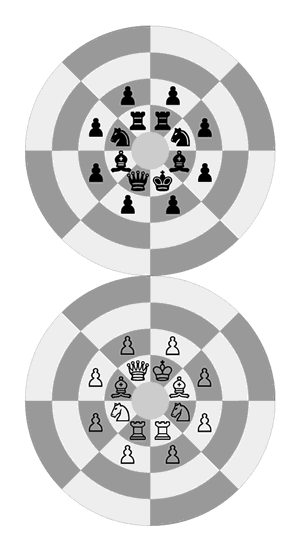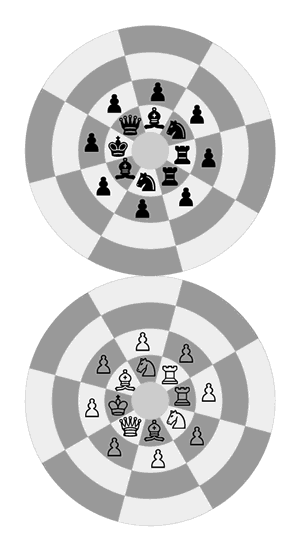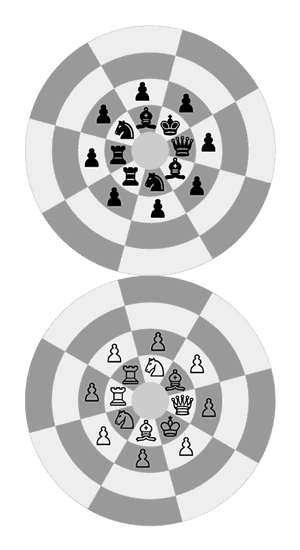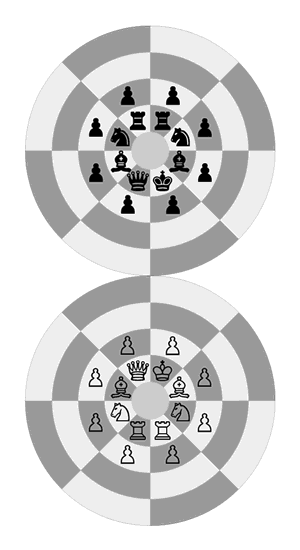
Now if I put all pieces in initial positions on the chessboard and the Dot, it will look like the diagram below:

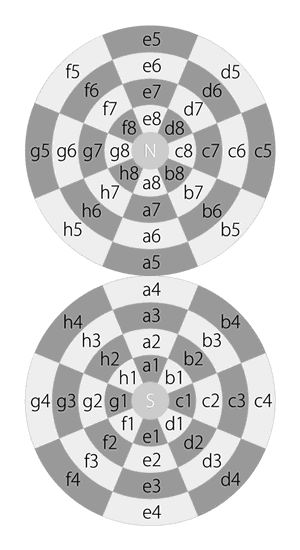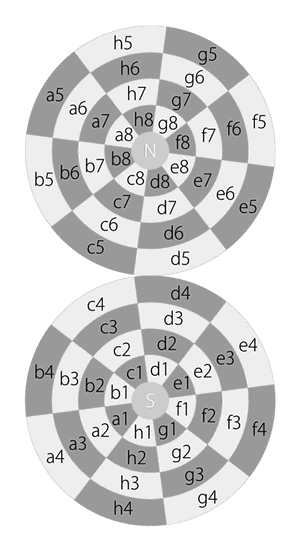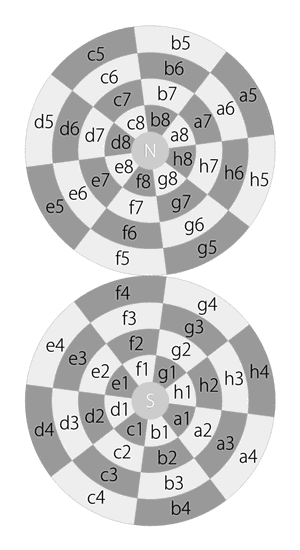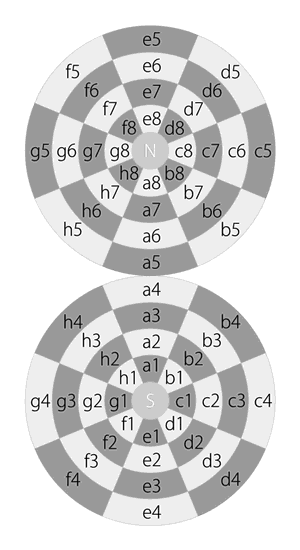
All pieces in initial positions on the chessboard and the Dot

It’s interesting that each side of pieces on the Dot surround their poles; white pieces surround the south pole, and black pieces surround the north pole.

The animation below shows the relation of pieces in initial positions on two hemispheres more accurately.

The relation of pieces in initial positions on two hemispheres

For future reference, the 8 squares alongside a pole are jointly called as “polar circle”. This noun will be mentioned later when it comes to “castling” and “pawn promotion” rules.

Before we get any further, I have to clarify the essence of the Dot.

Although the Dot is a 3-dimensional object, which has height, width and depth, however the “crust” of the Dot is just a 2-dimensional surface, without borders.

How to define the dimension of an object? It depends on how many sets of value is needed to pinpoint a location on that object. See this article for more information.

On a spherical surface, such as the surface of planet Earth, it takes two sets of value to pinpoint a location. For example, the coordinates of Eiffel Tower in Paris, France is (48°51’29.6”N, 2°17’40.2”E), and the coordinates of Great Pyramid of Giza in Egypt is (29°58’45.03”N, 31°08’03.69”E).

Likewise, it takes two sets of value to note a square on the chessboard or the Dot. For example, the square the white king occupies in initial position is (e, 1), and the square the black queen occupies in initial position is (d, 8). We simply use “e1” and “d8” for chess notation.

Since the “crust” of the Dot is essentially a 2-dimensional surface just like the flat chessboard, it must can be displayed as a 2-dimensional and rectangular chart just like the flat chessboard, can it not?

Yes, it can. And I call it “2DFARCSOD”, which stands for “2-Dimensional, Flat And Rectangular Chart of Squares On the Dot”.

Before I start to make a 2DFARCSOD, I need to put some colors on the chessboard in order to show the process as clear as possible.

My sincere apology to people with color vision deficiency, but color is the best way I can ever figure out to make this chart  as easy to understand as possible.

(Just for a quick memorize: North is red because it’s crowded. South is blue because it’s iced. West is green because it’s scientific. East is purple because it’s mysterious.)

A colored chessboard

It takes seven steps to make a 2DFARCSOD:

1)

2)

3)

4)

5)

6)

7)

Replicate infinite times of chessboard and make them all West-East connected, to create a stream of chessboards. We call this stream “ALPHA”.

Duplicate the stream “ALPHA”.

Perform horizontal reflection to the stream “ALPHA”, to make it only North-South reversed but not East-West reversed. We call this stream “BETA”.

Shift the stream “BETA” by 4 squares horizontally, to align rank a with e, b with f, c with g, and d with h.

Connect their South borders, to create a new stream. We call this stream “GAMMA”.

Duplicate the stream “GAMMA”, and connect their north borders.

Repeat step 6 infinite times, to eventually create a 2DFARCSOD, which is an infinite big, 2-dimensional chessboard continuum without border.

The making of 2DFARCSOD.

The relative positions between all squares on 2DFARCSOD are exactly the same as they are on the Dot.

The 2DFARCSOD is an infinite continuum because the surface of the Dot is border-less. The only way to make a border-less 2-dimensional chart is to make it infinite big.

By the way, you can use the same method to create a 2-dimensional, flat and rectangular chart of the surface of a terrestrial globe:

2-dimensional, flat and rectangular chart of the surface of a terrestrial globe

On the Dot, any piece moves along a fixed direction will find itself arriving at the very same square where it left from over and over again, because the piece is moving along a loop. The same thing happens on the 2DFARCSOD.

If an aircraft on the equator of planet Earth flies along latitude and keeps its heading straight, it will round the equator and eventually back to its starting point. Likewise, if a piece, e.g., a rook, on square d5 on the Dot moves along latitude and keeps its direction straight, it will pass e5, f5, g5, h5, a5, b5, c5 and eventually move back to d5.

Rook moves along latitude on the Dot

Now if I change the diagram above into the 2DFARCSOD, it looks like this:

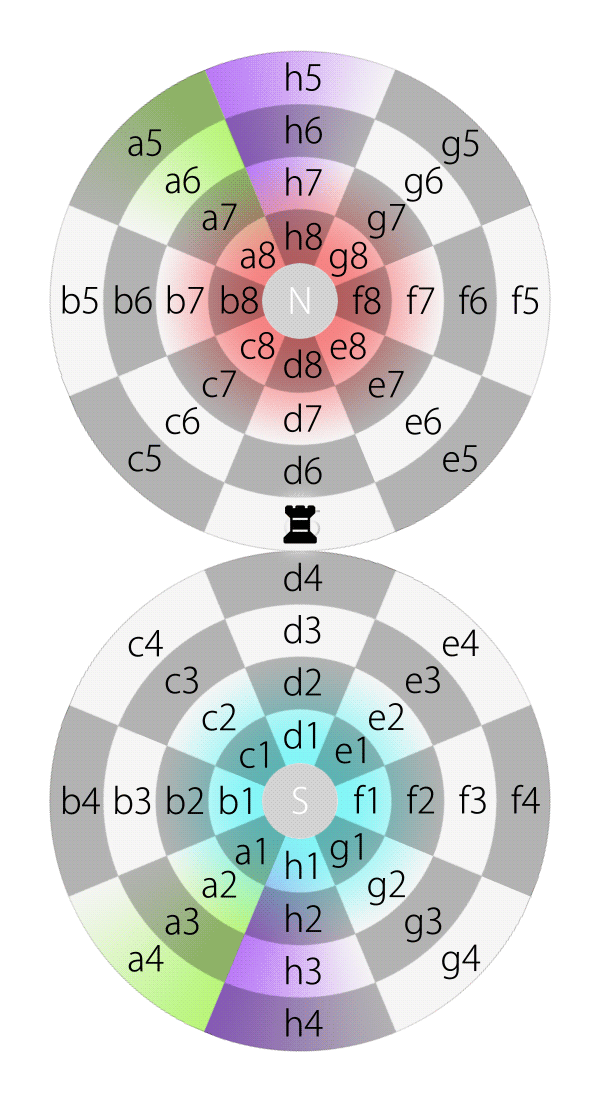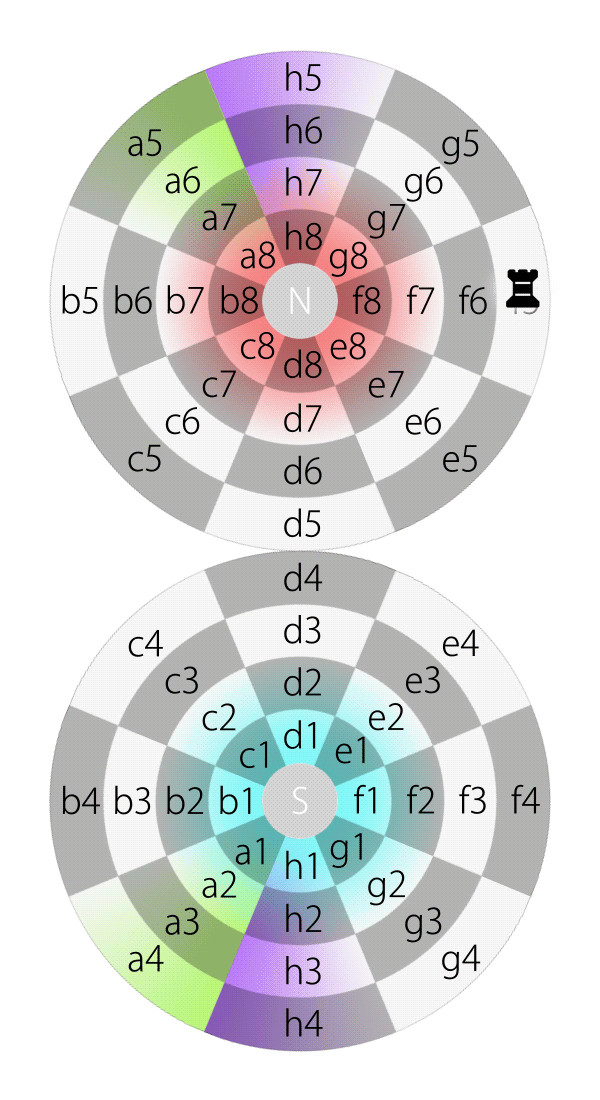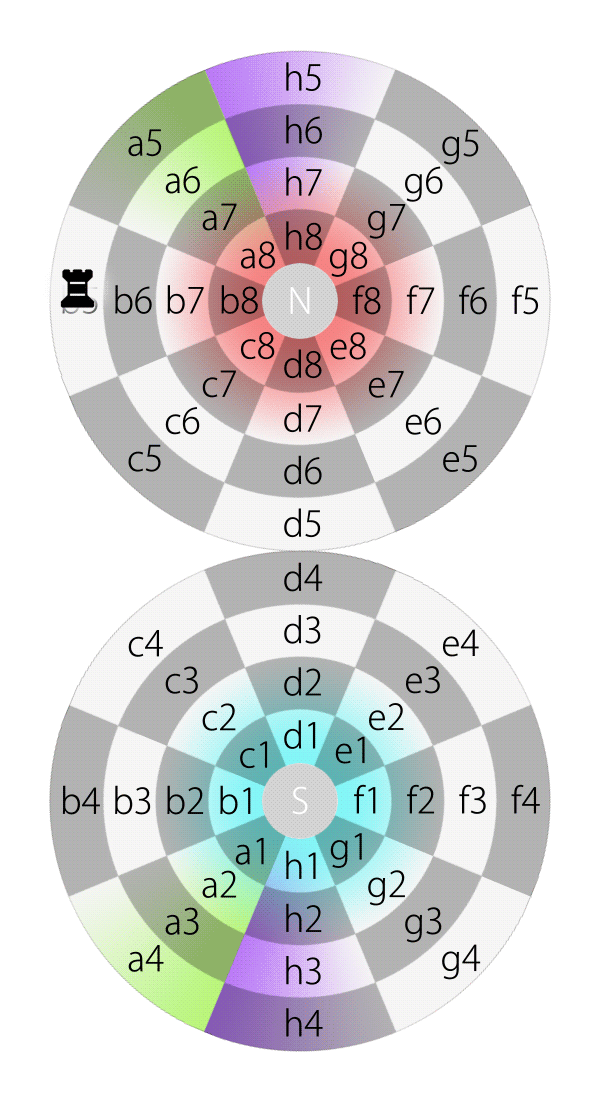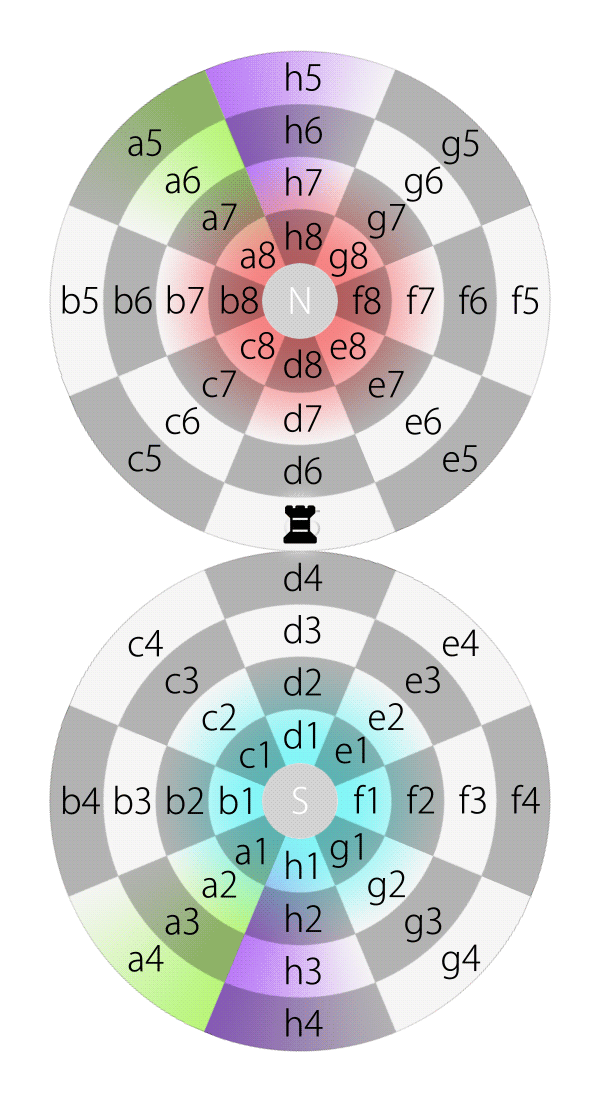
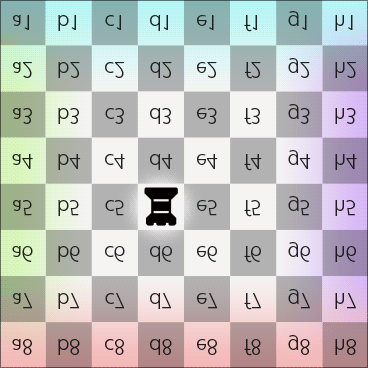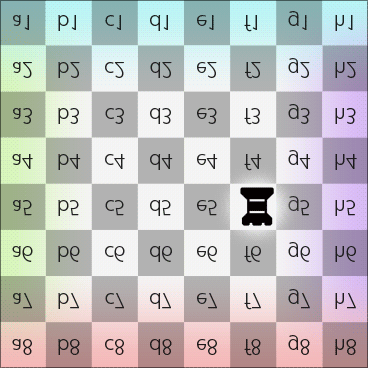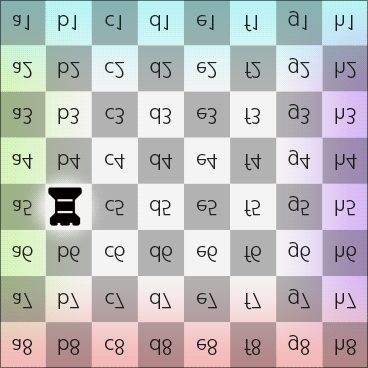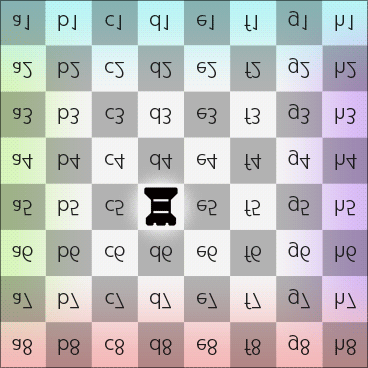
Rook moves along latitude on the Dot (in 2DFARCSOD view)

And here is the single-chessboard view:

Rook moves along latitude on the Dot (in 2DFARCSOD single-chessboard view)

In case of it’s not easy to notice, let me point it out that all the rooks on the 2DFARCSOD above are actually the same one, because all chessboards are in fact replicas from the single, original one.

If an aircraft on planet Earth flies along longitude and keeps its heading straight, it will reach a pole, and then another pole, and then eventually back to its starting point.

Likewise, if a piece, e.g., a rook, on square d7 on the Dot moves along longitude and keeps its direction straight, it will pass d8, N, h8, h7, h6, h5, h4, h3, h2, h1, S, d1, d2, d3, d4, d5, d6 and eventually move back to d7.

Rook moves along longitude on the Dot

Now if I change the diagram above into the 2DFARCSOD, it looks like this:

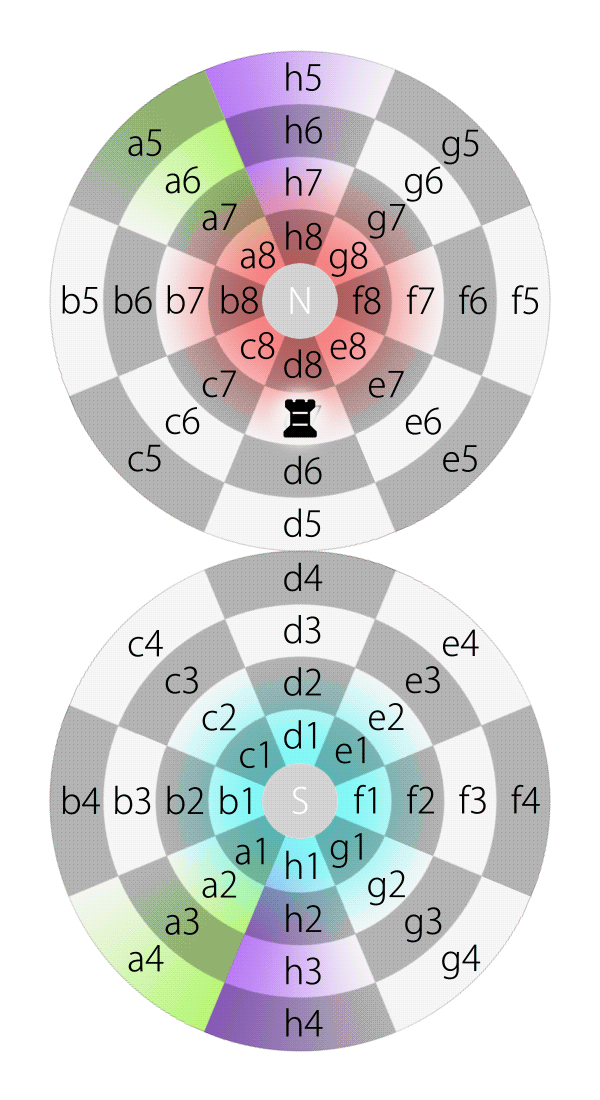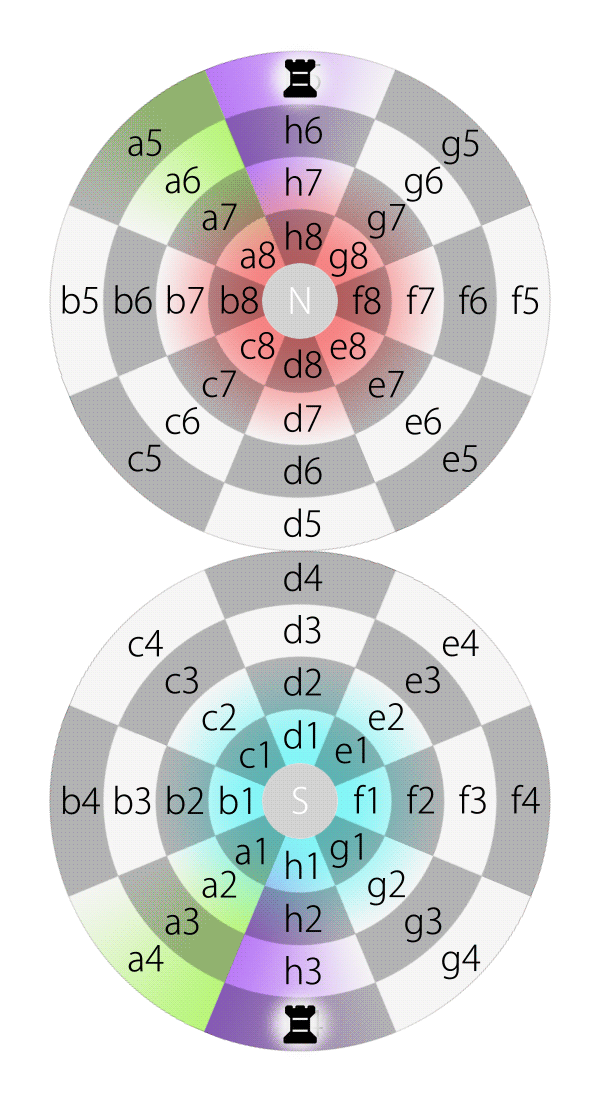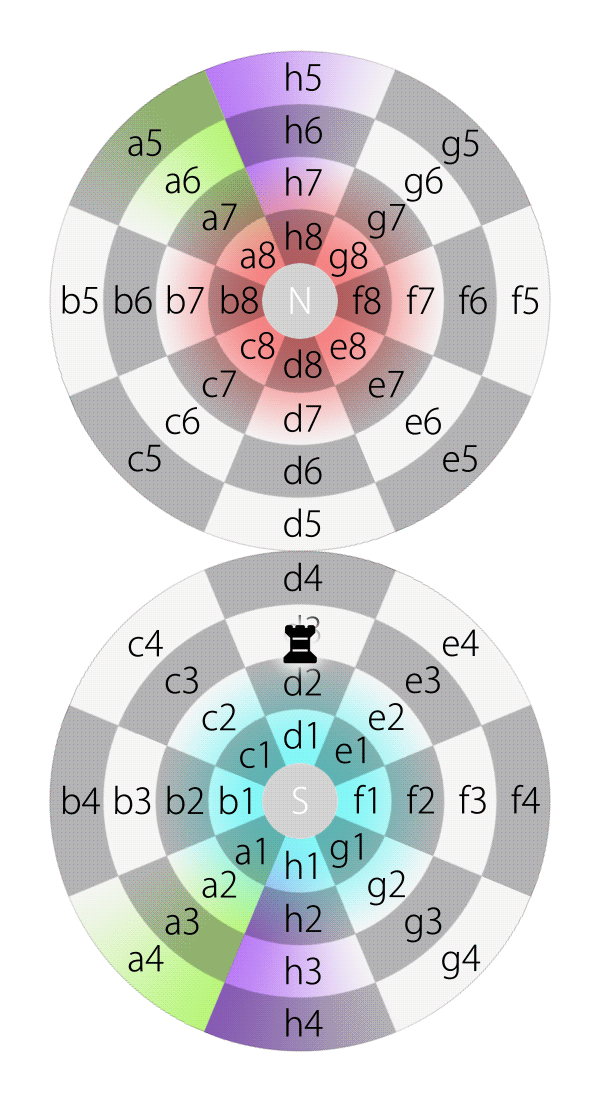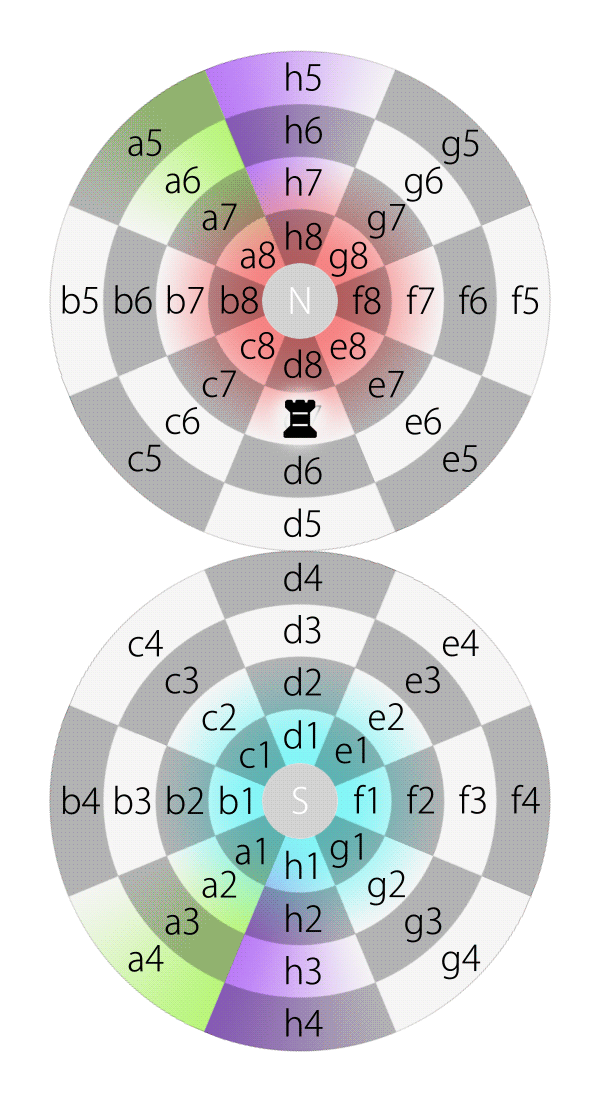
Rook moves along longitude on the Dot (in 2DFARCSOD view)

Likewise, all rooks on the 2DFARCSOD above are actually the same one, because all chessboards are in fact replicas from the single, original one.

And here is the single-chessboard view:

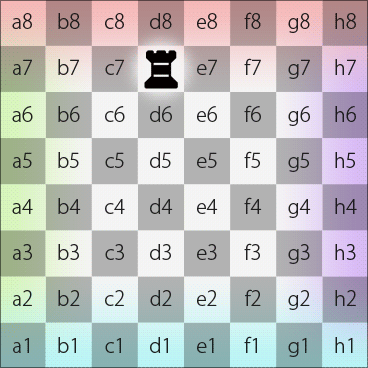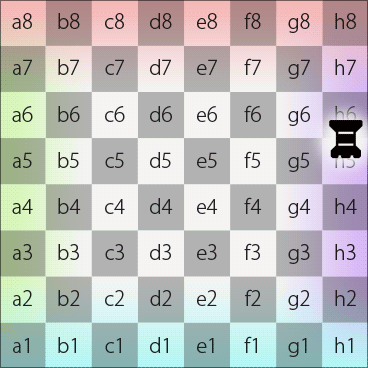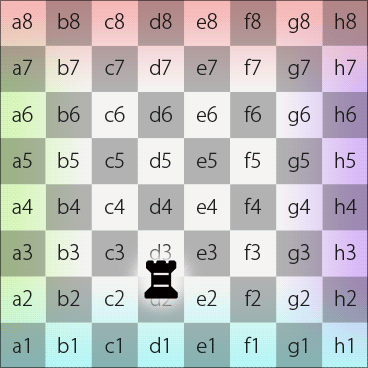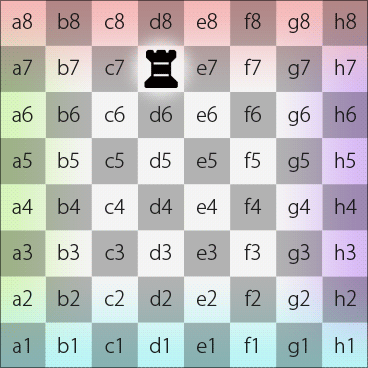
Rook moves along longitude on the Dot (in 2DFARCSOD single-chessboard view)

Due to the “North-South reversed” of some chessboards, the moving direction of piece is also North-South reversed when it pass the pole.

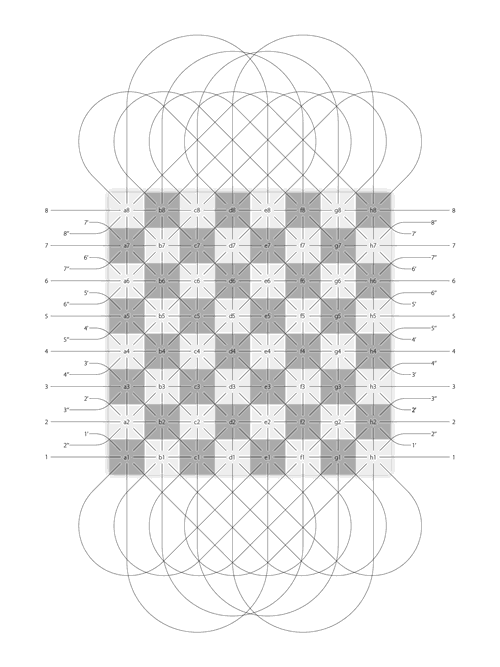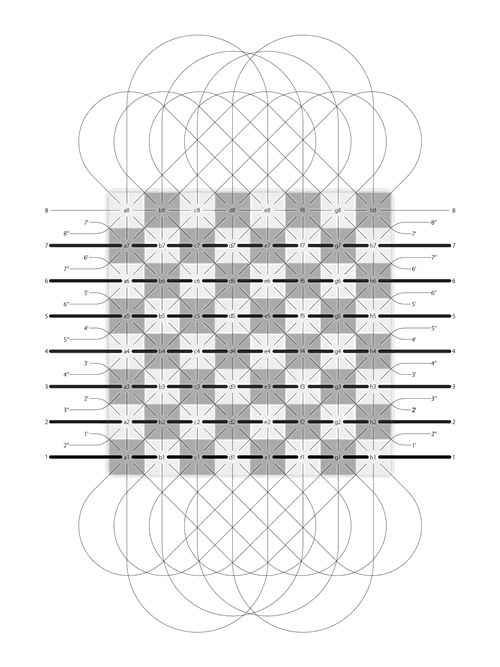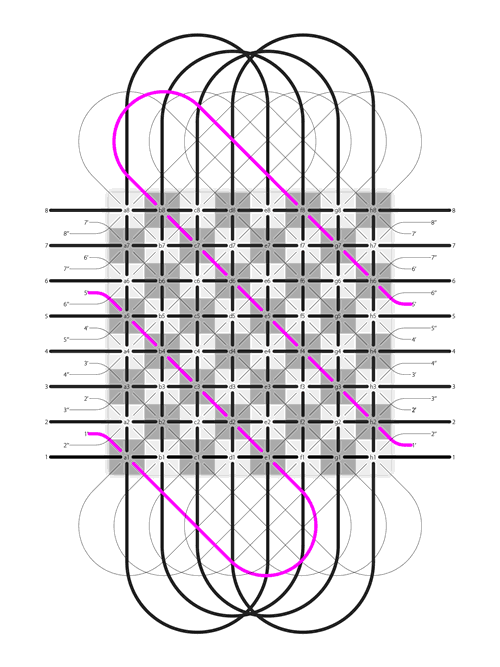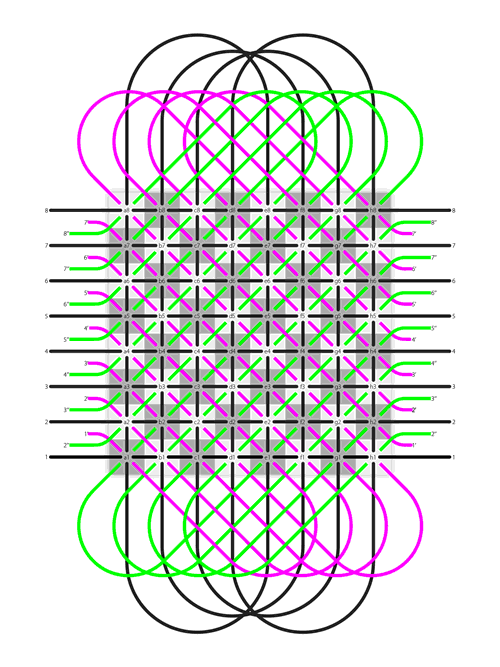
Now, we have already seen latitudinal loop and longitudinal loop of rook on the Dot. How about diagonal loop of bishop on the Dot?

Let’s figure it out. One step a time.

In this part, I have to show the route on 2DFARCSOD first. And in order to show it as clear as possible, I put magenta lines on the chart to visualize the routes.

Step 1 of 3: If a piece, e.g., a bishop, on square d2 on the Dot and moves along diagonal toward North-East, the route on 2DFARCSOD looks like this:

Bishop starts its journey by moving toward North-East (in 2DFARCSOD view).

Step 2 of 3: According to the chess rule, “A bishop always moves on squares with the same color”. Therefore, after the bishop passes the North pole, it should still be on a black square and moves toward South, which means it can only move toward South-West. Now the route looks like this:

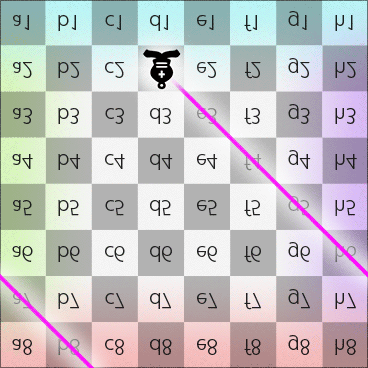
After passes the North pole, the bishop moves toward South-West (in 2DFARCSOD view).

Step 3 of 3: According to the previously mentioned rule, after the bishop passes the South pole, it should still be on a black square and moves toward North, which means it can only move toward North-East, and that allows the bishop back to its starting square d2. Now the route looks like this:

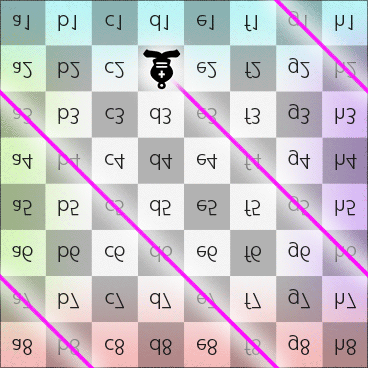
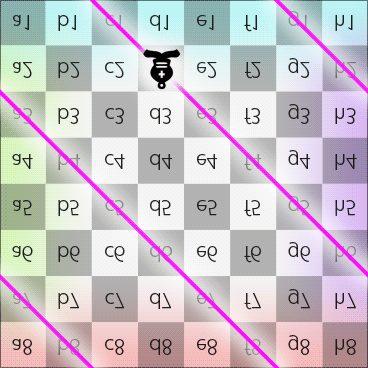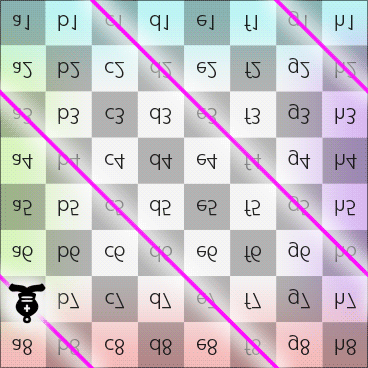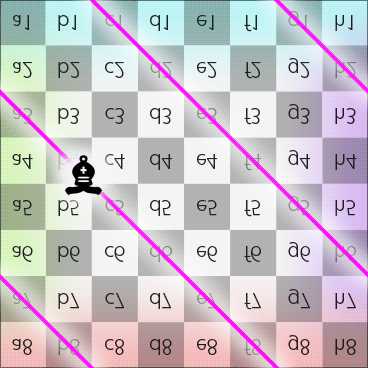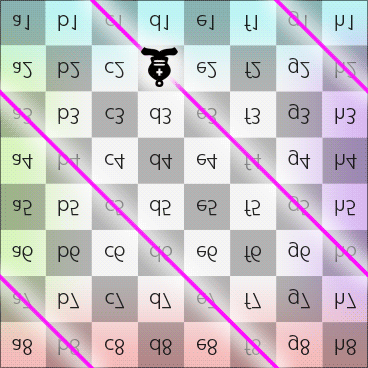
Bishop moves along diagonal on the Dot (in 2DFARCSOD view)

So, the bishop starts from d2 and then passes e3, f4, g5, h6, a7, b8, N, f8, e7, d6, c5, b4, a3, h2, g1, S, c1 and eventually moves back to d2.

And here is the single-chessboard view:

Bishop moves along diagonal on the Dot (in 2DFARCSOD single-chessboard view)

And here is the diagram of diagonal loop on the Dot:

Bishop moves along diagonal on the Dot

The diagonal loop is some kind of spiral on the diagram. And this route keeps bishop always on the squares with the same color.

Finally, it’s time to answer the big question: How is it possible to play chess on a spherical chessboard with the traditional rules?

Answer: According to the explanation above, the essence of the surface of the spherical chessboard (a.k.a. the Dot) can be considered as 2-dimensional, flat and rectangular. So all rules of chess can perfectly apply to it without change.

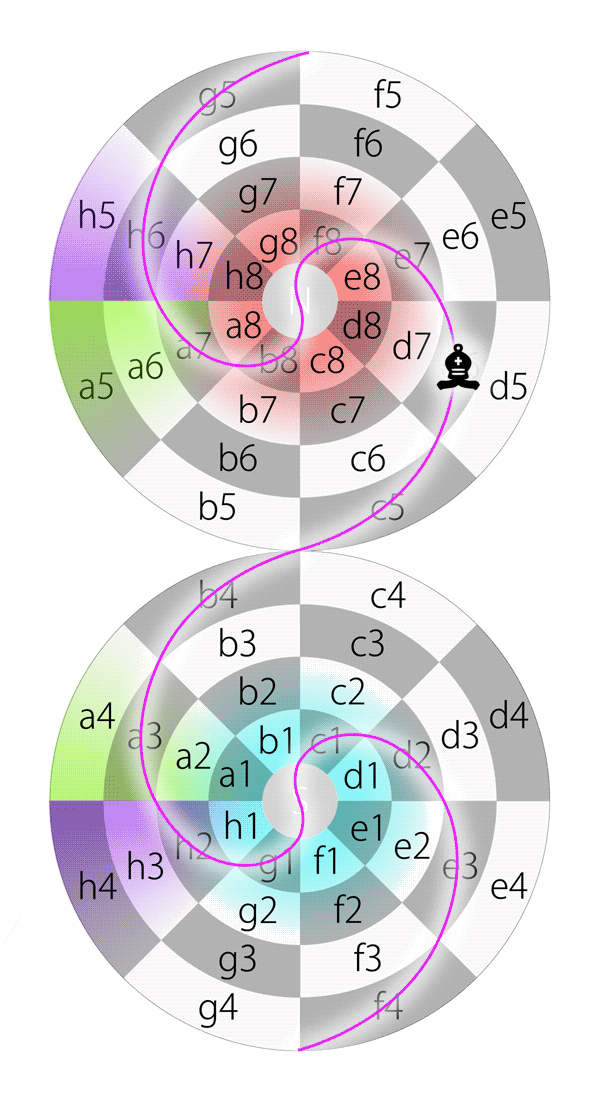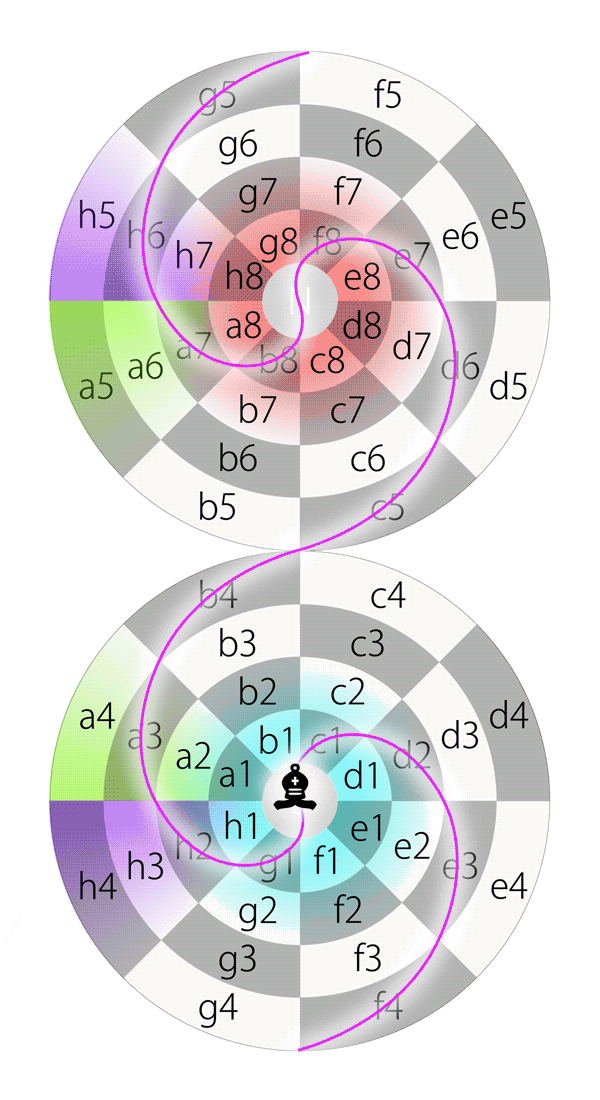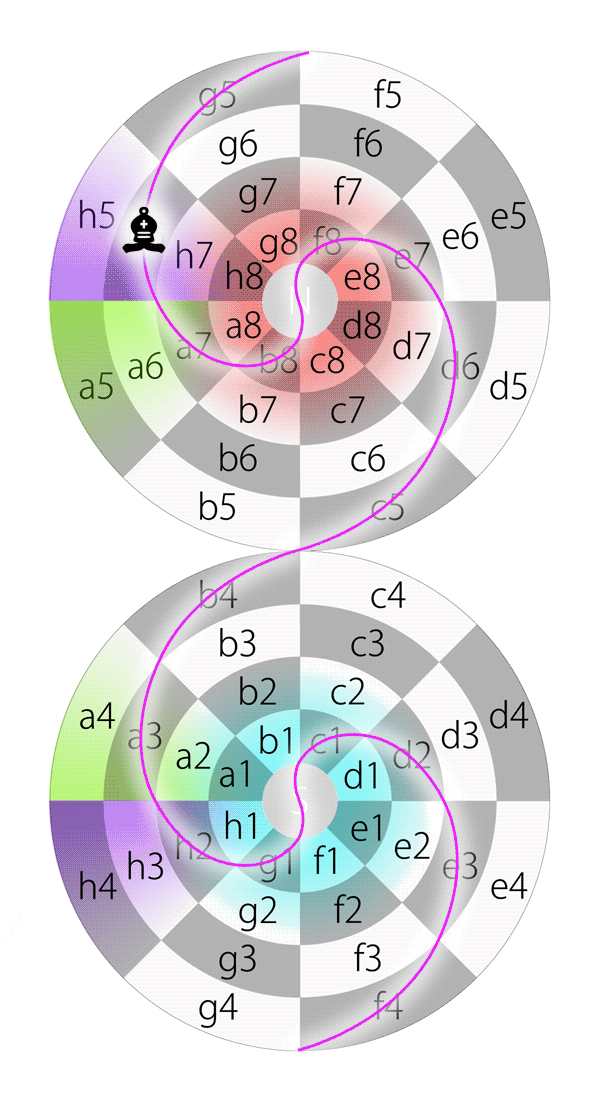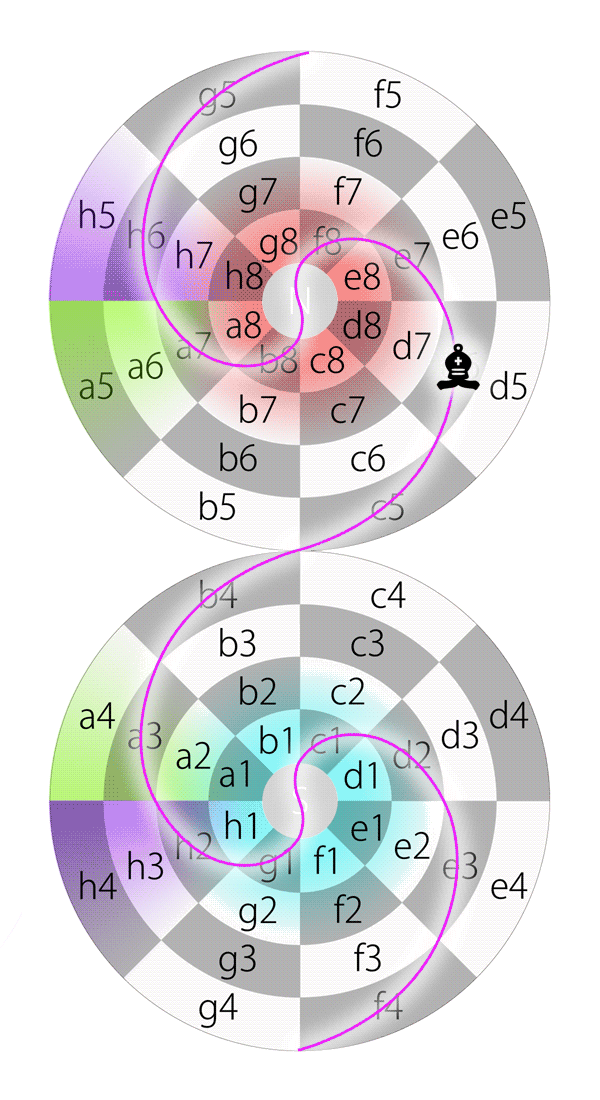
The total 20 loops on the Dot (in the single-chessboard view)

The following rules in texts are exactly the same to traditional chess rules, and the diagrams are the implementations of traditional chess rules on the Dot.

On the diagrams, little black dots on the squares mark the piece’s destinations. Lines between piece and dots mark all routes from piece to its destinations.

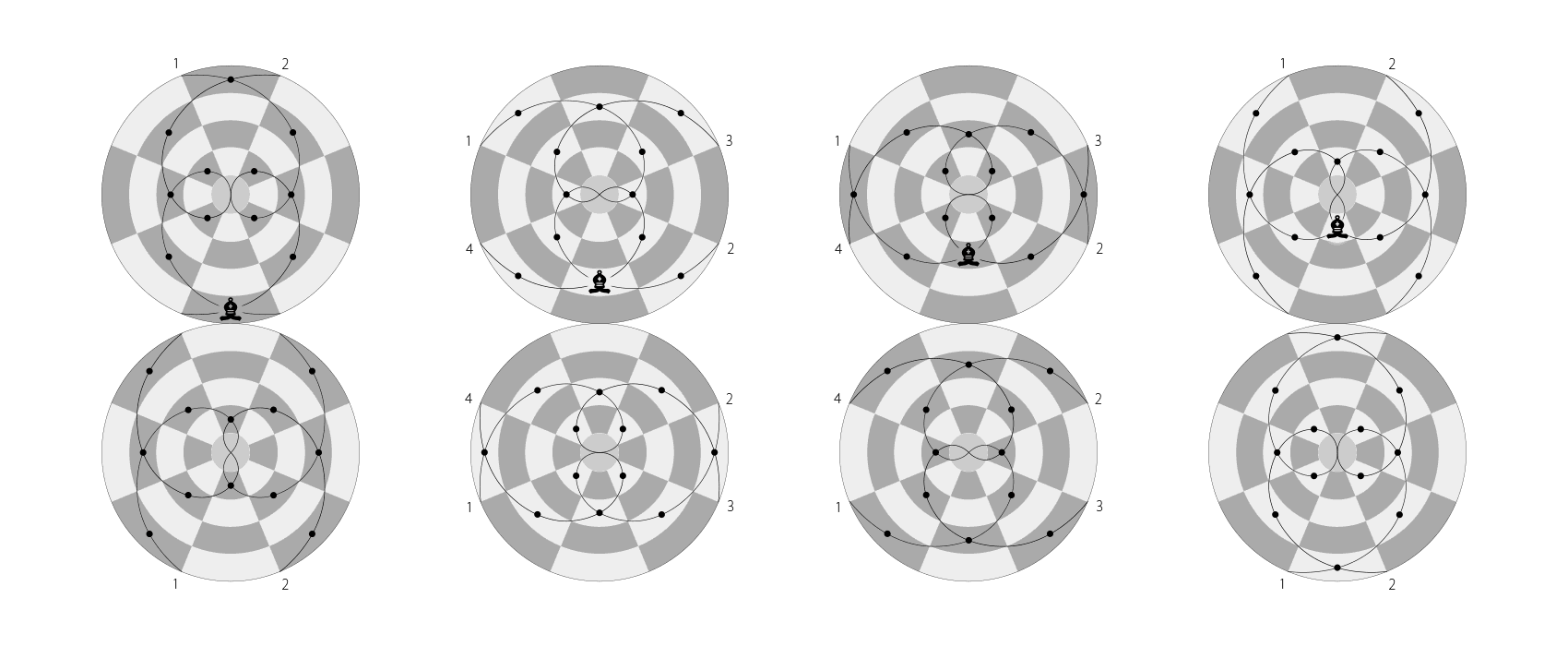
The ROOK can move any number of squares along any rank (latitude) or file (longitude), but may not leap over other pieces. It moves the same way when capture an opponent’s piece.

Rook’s move and capture on the Dot

The BISHOP can move any number of squares along any diagonal, but may not leap over other pieces. It moves the same way when capture an opponent’s piece.

Bishop’s move and capture on the Dot

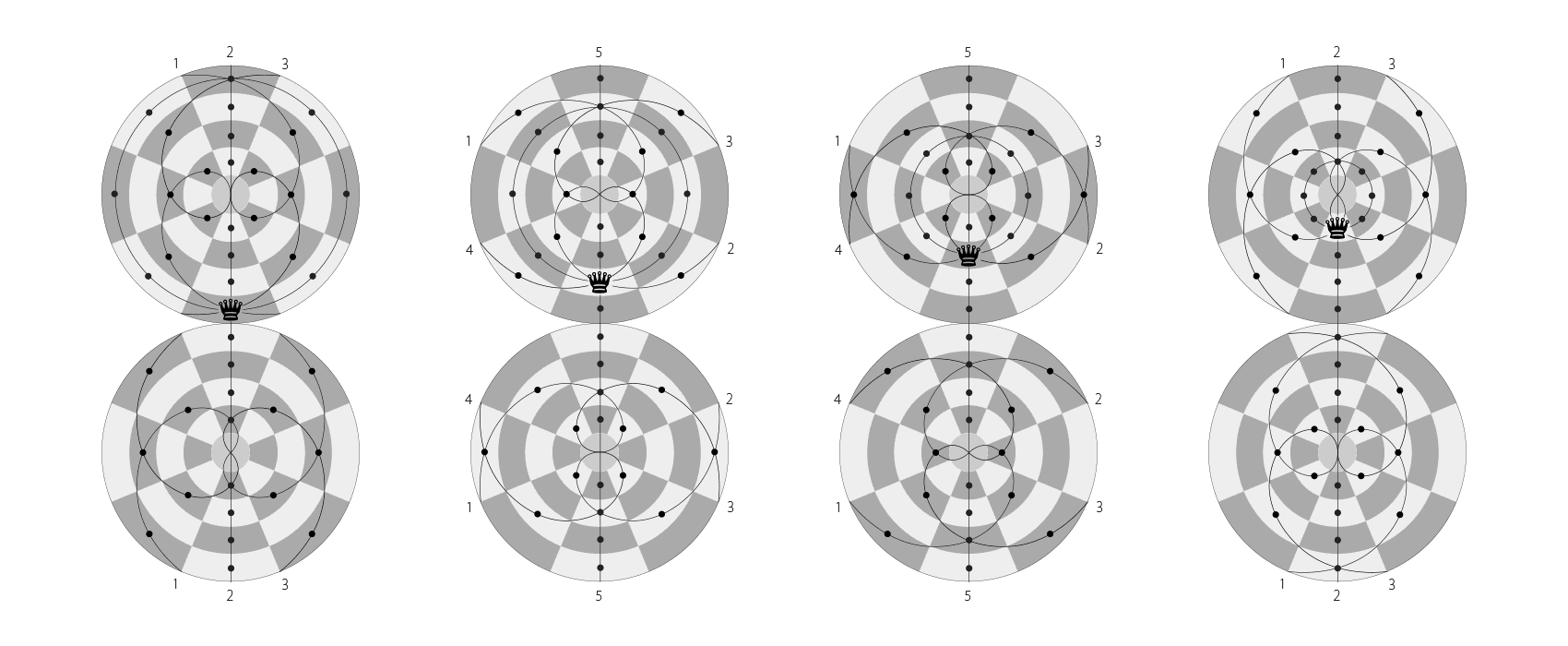
The QUEEN can move any number of squares along any rank (latitude), file (longitude) or diagonal, but may not leap over other pieces. It moves the same way when capture an opponent’s piece.

Queen’s move and capture on the Dot

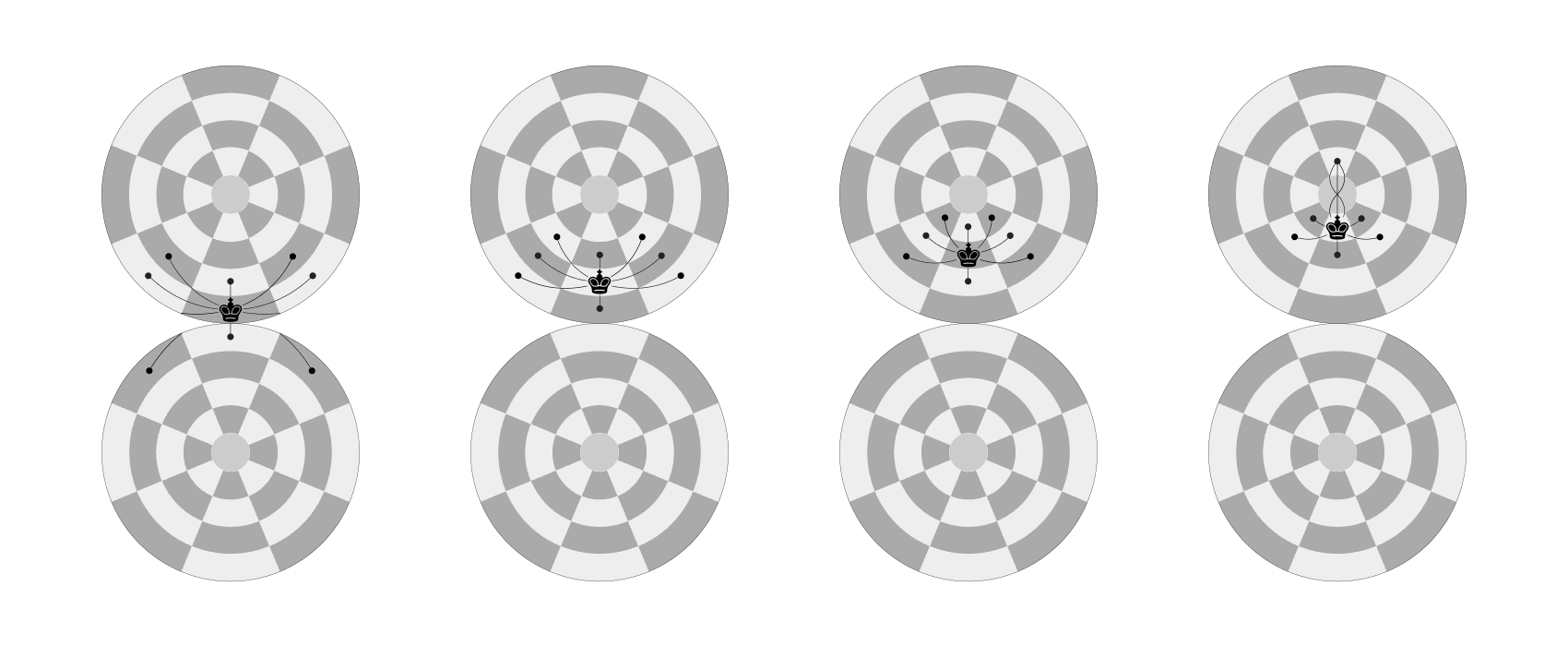
The KING can move only one square along any rank (latitude), file (longitude) or diagonal. It moves the same way when capture an opponent’s piece.

King’s move and capture on the Dot

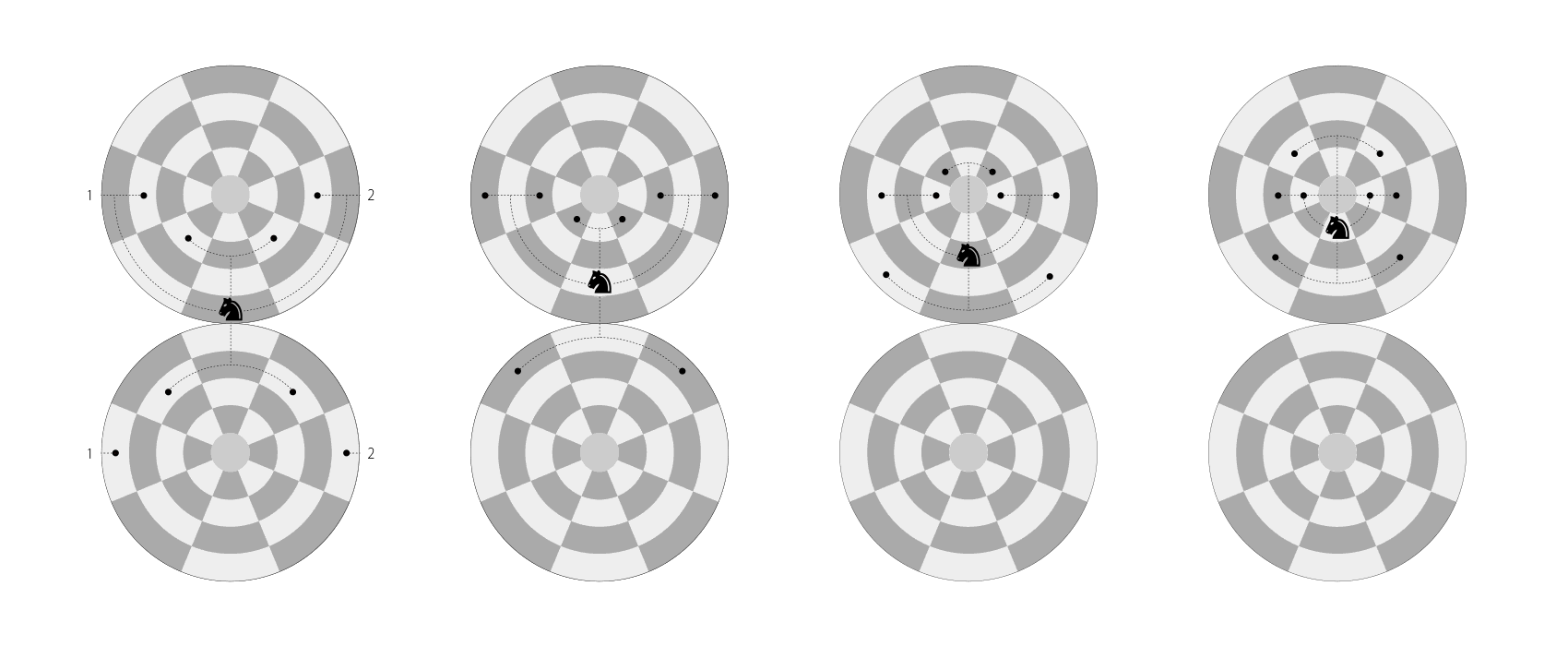
The KNIGHT can move to any of the closest squares that are not on the same rank (latitude), file (longitude), or diagonal, thus the move forms an “L-shape”: two squares along rank (latitude) and one square along file (longitude), or one square along rank (latitude) and two squares along file (longitude). The KNIGHT is the only piece that can leap over other pieces. It moves the same way when capture an opponent’s piece.

Knight’s move and capture on the Dot

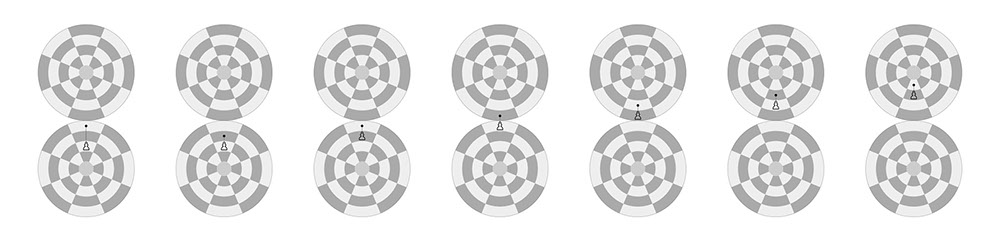
The PAWN may move forward (approach to opponent’s pole) to the unoccupied square immediately in front of it on the same file (longitude), or on its first move it may advance two squares along the same file (longitude) provided both squares are unoccupied. The PAWN may not move backwards (away from opponent’s pole).

Pawn’s move on the Dot

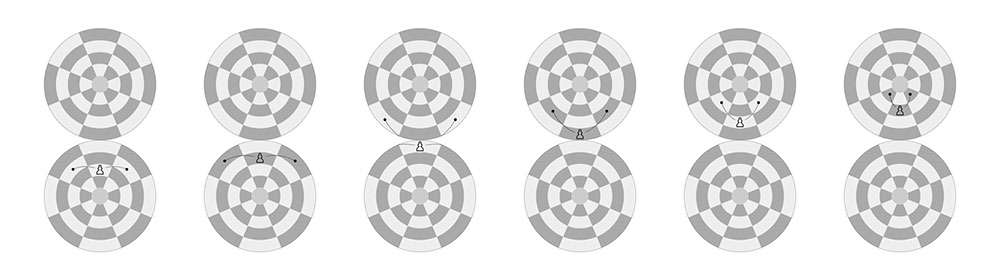
The PAWN may capture an opponent’s piece on a square diagonally in front (approach to opponent’s pole) of it on an adjacent file (longitude), by moving to that square. The PAWN may not move to these squares if they are vacant.

Pawn’s capture on the Dot

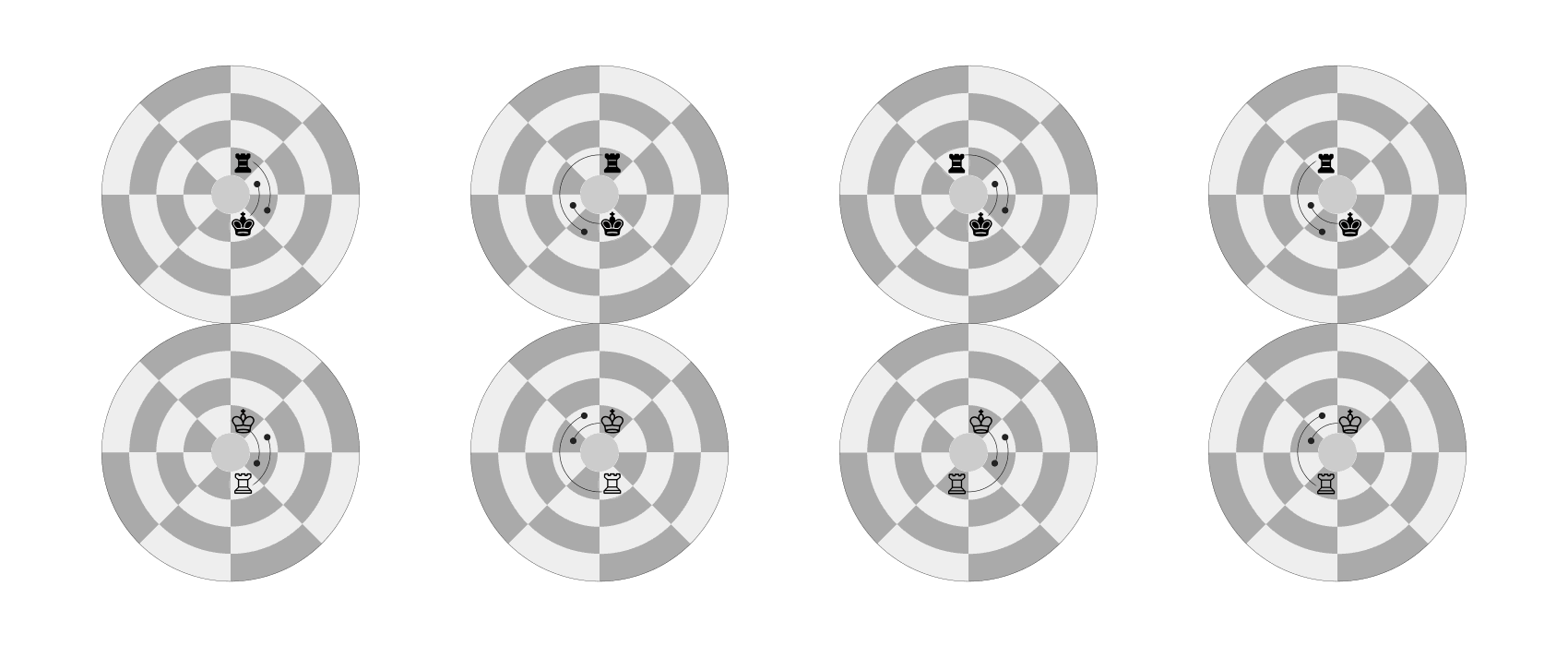
Castling: This consists of moving the KING two squares along the “polar circle” toward a ROOK and then placing the ROOK on the last square the KING has just crossed.

Castling on the Dot

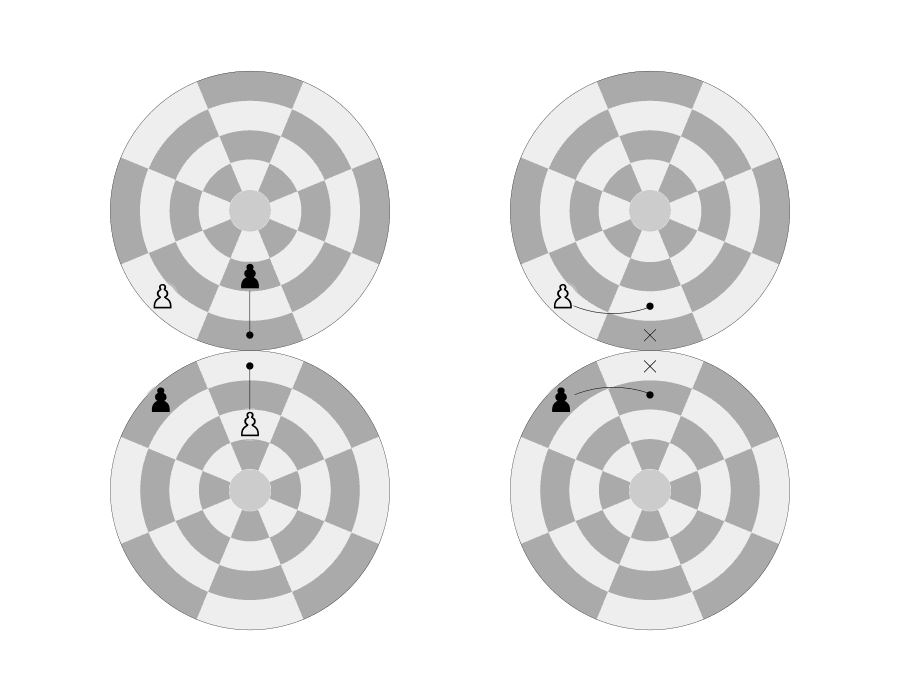
En passant: A special PAWN capture which can occur immediately after a player makes a double-step move from its starting position, and an opponent’s PAWN could have captured it had the PAWN moved only one square forward (approach to opponent’s pole).

En passant on the Dot

Promotion: The transformation of a PAWN that reaches its opponent’s “polar circle” into the player’s choice of a QUEEN, KNIGHT, ROOK, or BISHOP of the same color. Every PAWN that reaches its eighth rank (opponent’s polar circle) must be promoted.

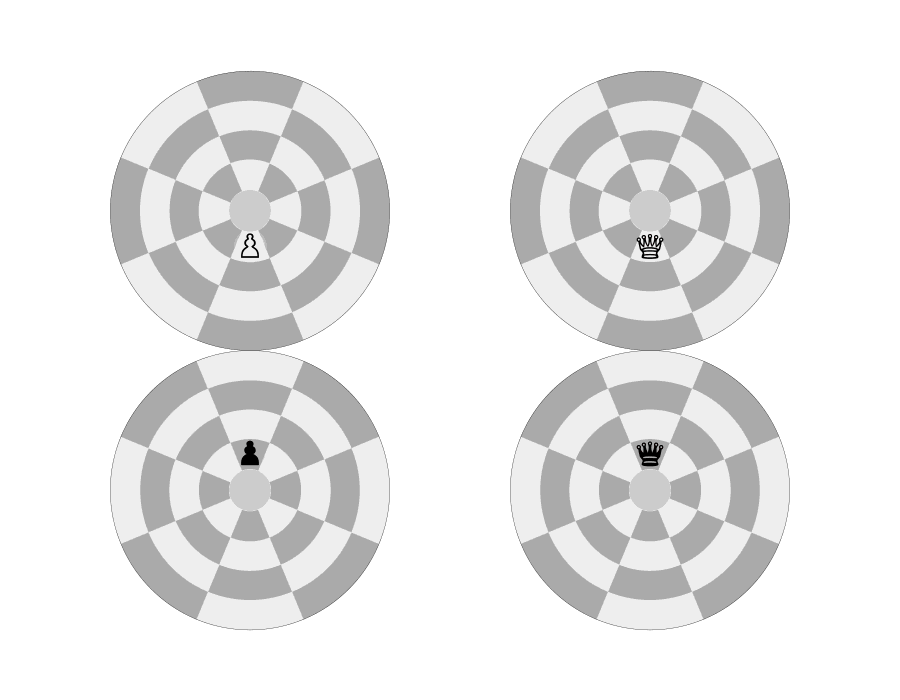
Promotion on the Dot

To sun up, the only difference between “Chess” and “Chess on the Dot ” is the topological shape of the chessboard. A chess player can play “Chess on the Dot” without learning any new rules.

The End

< Back to the main page of “Chess on the Dot”